1 ~ n까지 합(등차수열의 합)을 구하는 원리

정의

등차수열의 합은 연속하는 항들 간의 차이가 일정한 수열의 합을 말합니다. 등차수열의 합을 구하는 공식을 사용하여 1부터 n까지의 합을 계산할 수 있습니다.

사용 방법

등차수열의 합을 구하기 위해서는 다음과 같은 공식을 사용합니다:

(첫 번째 항 + 마지막 항) × 항의 개수 / 2

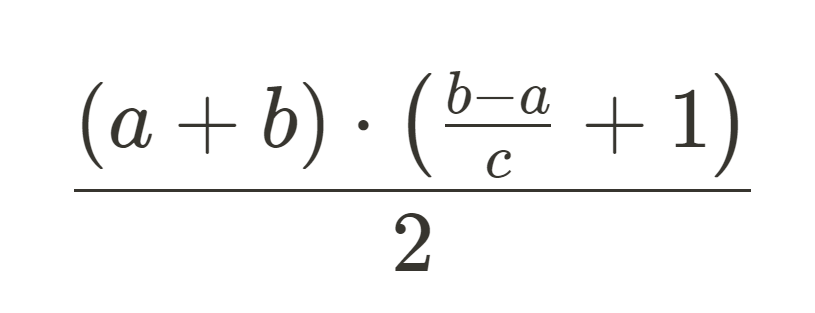
a: 시작값

b: 종료값

c: 공차

공차: 등차수열에서 연속하는 항들 간의 차이

수학 예제

1부터 10까지의 합을 구한다고 한다면,

a: 시작값= 1

b: 종료값= 10

c: 공차= +1

이므로 대입을 한다면 아래와 같습니다.

장점

• 등차수열의 합 공식은 간단하고 직관적입니다.
• 큰 수의 합을 빠르게 계산할 수 있습니다.
• 일반적인 형태의 등차수열에 대해 적용 가능합니다.

단점

• 이 공식은 등차수열에만 적용 가능하며, 다른 유형의 수열에는 적용할 수 없습니다.
• 항의 개수를 알아야 공식을 사용할 수 있습니다.

자바 예제

public class ArithmeticSeriesSum {
    public static void main(String[] args) {
				int start = 1;
        int end = 10;
        int commonDifference = 1;
        int sum = (start + end) * ((end - start) / commonDifference + 1) / 2;
        System.out.println("1부터 10까지의 합: " + sum);
    }
}