반응형
정의
최소 공통 조상, LCA(Lowest Common Ancestor).
LCA는 트리 구조에서 두 노드의 가장 가까운 공통 조상을 찾는 알고리즘 또는 개념입니다.
예제

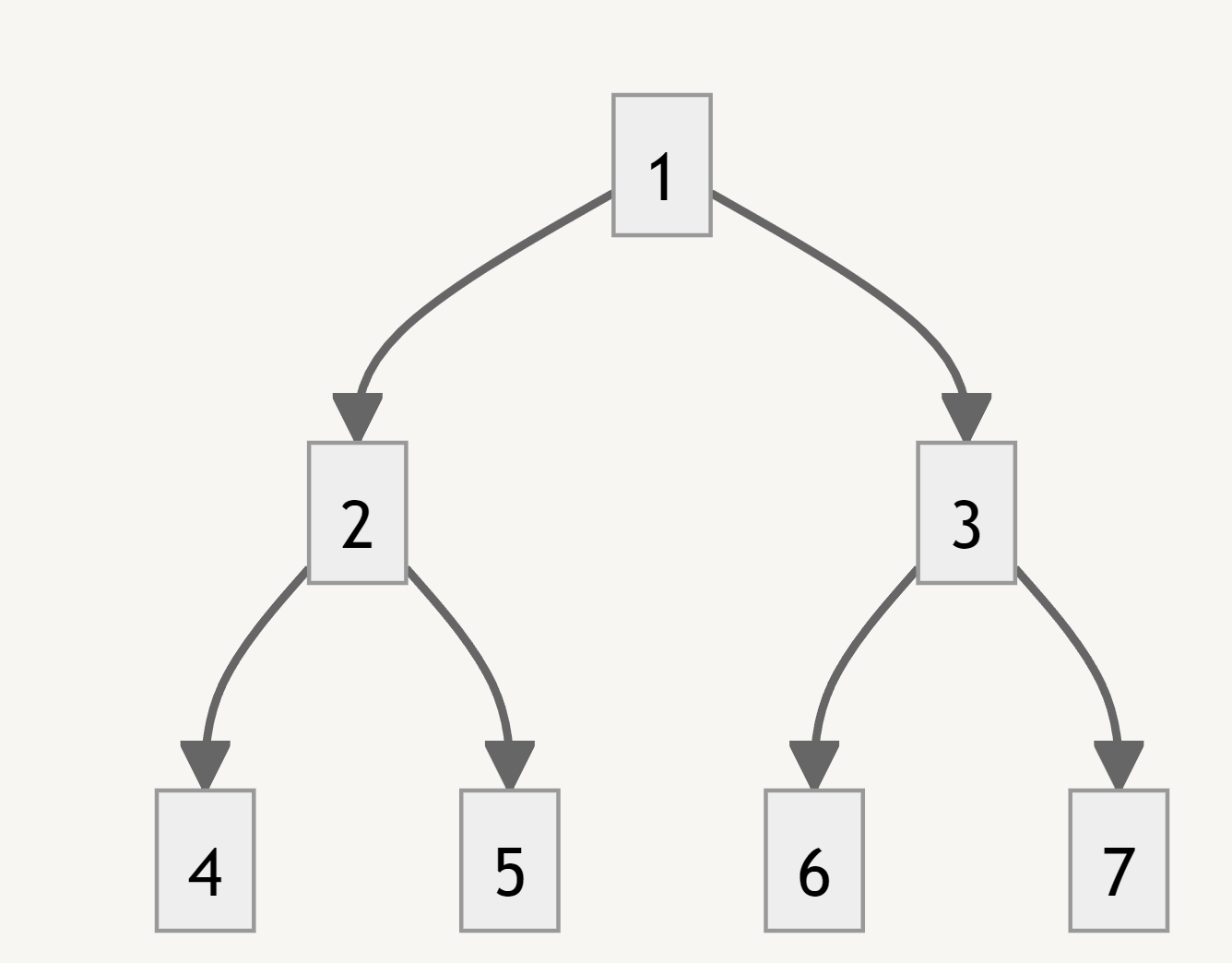
위와 같은 이진트리가 있다고 할때, 4와 6의 LCA는 1입니다.
LCA(4,6)=1
목적
LCA의 목적은 트리 구조에서 두 노드의 가장 가까운 공통 조상을 효율적으로 찾는 것입니다.
사용을 고려해야 하는 경우
LCA 알고리즘을 고려해야 하는 경우:
- 트리 구조에서 두 노드 간의 거리를 계산해야 할 때
- 특정 노드를 루트로 하는 서브트리에 속한 노드들을 찾아야 할 때
- 컴퓨터 네트워크에서 최단 경로를 계산해야 할 때
- 게임 개발에서 충돌 감지 등의 문제를 해결해야 할 때
사용하면 안되는 경우
LCA 알고리즘은 트리 구조가 아닌 다른 자료 구조에서는 사용할 수 없습니다. 또한, 트리 구조가 아니더라도 두 노드의 공통 조상을 찾는 문제가 아니라면 LCA를 사용할 필요가 없습니다.
장점
- 효율적인 시간 복잡도로 두 노드의 LCA를 찾을 수 있습니다.
- 전처리(preprocessing) 단계를 거친 후 쿼리(query)를 빠르게 수행할 수 있습니다.
단점
- LCA 알고리즘은 트리 구조에 한정된 알고리즘이기 때문에, 다른 자료 구조에 적용할 수 없습니다.
구현 하는 법
- 이진트리의 각 노드의 부모와 깊이정보를 계산합니다.
- 위 과정을 전처리(preprocessing) 단계라고 합니다.
- LCA를 찾을려는 두 노드의 부모로 이동을 합니다
- 이동을 하며, 각 노드의 교차점이 있는지 확인을 합니다
- 최초로 일어나는 교차점이 LCA입니다.
예제
import java.util.ArrayList;
import java.util.List;
class Node {
int value;
Node parent; // 부모 노드를 저장하기 위한 변수
List<Node> children; // 자식 노드들을 저장하기 위한 리스트
Node(int value) {
this.value = value;
this.children = new ArrayList<>();
}
}
public class LCAExample {
// 전처리 작업을 수행하는 메서드
private static void preprocess(Node node, Node parent, int depth) {
node.parent = parent; // 현재 노드의 부모 노드 정보 저장
for (Node child : node.children) {
preprocess(child, node, depth + 1); // 재귀적으로 자식 노드에 대해 전처리 작업 수행
}
}
// 최소 공통 조상을 찾는 메서드
private static Node findLCA(Node node1, Node node2) {
int depth1 = getDepth(node1); // 노드1의 깊이 계산
int depth2 = getDepth(node2); // 노드2의 깊이 계산
// 깊이를 맞추기 위해 더 깊은 노드를 위로 올림
while (depth1 > depth2) {
node1 = node1.parent;
depth1--;
}
while (depth2 > depth1) {
node2 = node2.parent;
depth2--;
}
// 공통 조상 찾기
while (node1 != node2) {
node1 = node1.parent;
node2 = node2.parent;
}
return node1; // 최소 공통 조상 반환
}
// 노드의 깊이를 계산하는 메서드
private static int getDepth(Node node) {
int depth = 0;
while (node.parent != null) {
node = node.parent;
depth++;
}
return depth;
}
public static void main(String[] args) {
// 트리 생성
Node root = new Node(1);
Node node2 = new Node(2);
Node node3 = new Node(3);
Node node4 = new Node(4);
Node node5 = new Node(5);
Node node6 = new Node(6);
Node node7 = new Node(7);
root.children.add(node2);
root.children.add(node3);
node2.children.add(node4);
node2.children.add(node5);
node3.children.add(node6);
node3.children.add(node7);
// 전처리 작업 수행
preprocess(root, null, 0);
// 최소 공통 조상 찾기
Node lcaNode = findLCA(node4, node5);
System.out.println("LCA: " + lcaNode.value); // 2
lcaNode = findLCA(node4, node6);
System.out.println("LCA: " + lcaNode.value); // 1
lcaNode = findLCA(node3, node7);
System.out.println("LCA: " + lcaNode.value); // 3
}
}
반응형
'old > Programming' 카테고리의 다른 글
| 재귀 함수 짜는 법 (0) | 2023.08.18 |
|---|---|
| 파이썬의 연산자 정리 (0) | 2023.08.10 |
| 단축 평가 계산(Short Circuit Evaluation)이란 (0) | 2023.07.31 |
| 자바 오브젝트 생성시, this 키워드를 사용하는 이유 (0) | 2023.07.30 |
| Gradle과 Maven을 IntelliJ IDEA에 설정하는 법 (0) | 2023.07.20 |